Le api usano gli esagoni per una semplice ragione: è la forma più efficiente in natura per la costruzione. Una griglia esagonale utilizza la minor quantità di materiale—in questo caso, cera—per creare un reticolo di celle con il massimo spazio di stoccaggio possibile e integrità strutturale. È una soluzione perfetta affinata da milioni di anni di evoluzione.
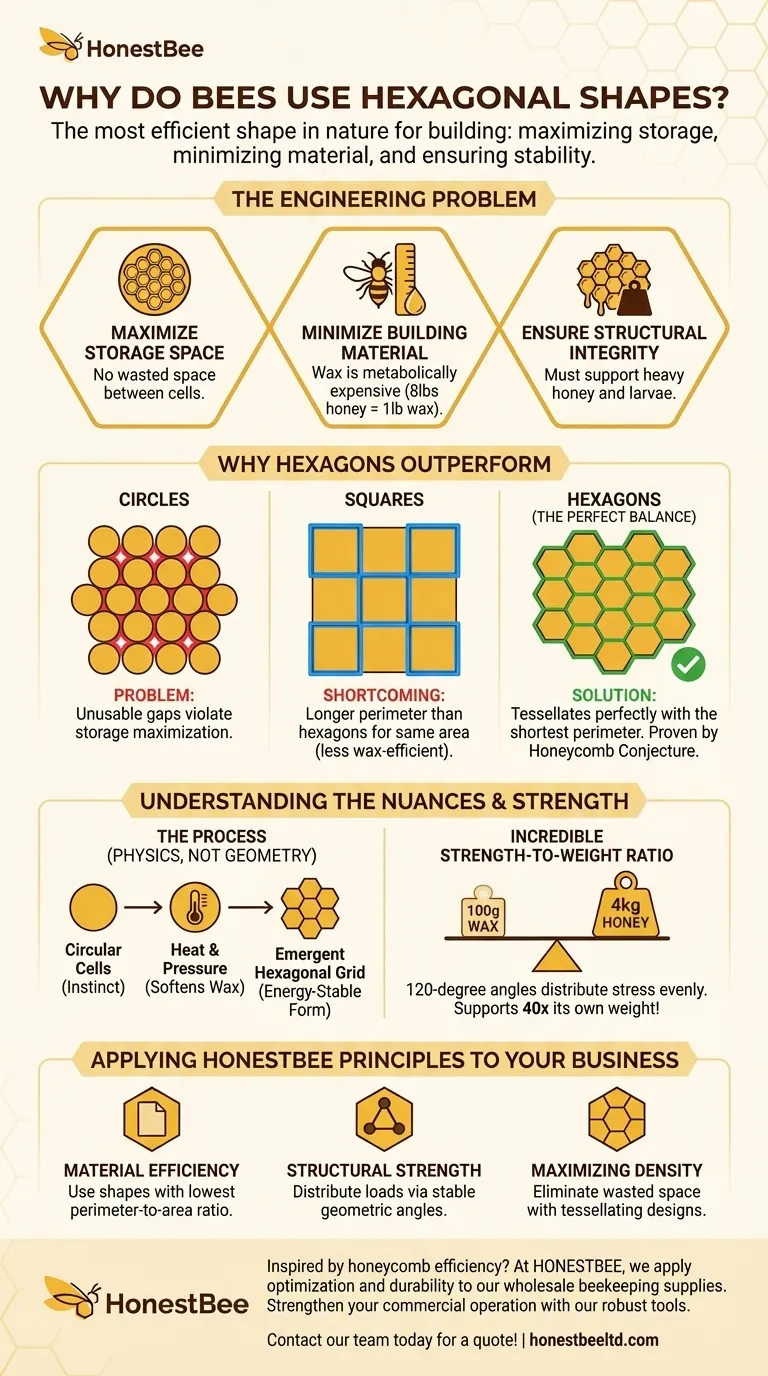
L'esagono del favo non è una scelta casuale; è la soluzione matematicamente ottimale a un complesso problema di ingegneria. Rappresenta il compromesso perfetto tra la minimizzazione dei materiali da costruzione, la massimizzazione della capacità di stoccaggio e la garanzia della stabilità strutturale.
Il Problema di Ingegneria che le Api Devono Risolvere
Per comprendere il genio dell'esagono, dobbiamo prima capire le sfide che le api affrontano. Hanno bisogno di una struttura che soddisfi tre requisiti ingegneristici critici.
Massimizzare lo Spazio di Stoccaggio
La sopravvivenza di una colonia dipende dall'immagazzinare quanto più miele e polline possibile. La forma delle celle di stoccaggio deve quindi essere efficiente in termini di spazio, senza lasciare spazi vuoti tra di esse.
Minimizzare il Materiale da Costruzione
Le api devono consumare circa otto libbre di miele per produrre solo una libbra di cera d'api. Questo rende la cera una risorsa metabolicamente costosa che non può essere sprecata in un design inefficiente. La forma ideale deve racchiudere una data area con il perimetro più corto possibile.
Garantire l'Integrità Strutturale
Un favo finito è incredibilmente pesante. La struttura deve essere abbastanza forte da sostenere non solo il peso del miele ma anche le larve di api in via di sviluppo, il tutto mentre è costruita con un materiale relativamente fragile.
Perché gli Esagoni Superano le Altre Forme
Quando valutato rispetto a queste esigenze, l'esagono emerge come l'unica forma che soddisfa perfettamente tutte le condizioni. Altre forme comuni, come cerchi e quadrati, presentano difetti critici.
Il Problema con i Cerchi
Un cerchio è tecnicamente la forma più efficiente per contenere la massima area con il minimo perimetro. Tuttavia, quando i cerchi sono impacchettati insieme, lasciano spazi inutilizzabili, violando la necessità di massimizzare lo spazio di stoccaggio.
La Mancanza dei Quadrati
Quadrati, triangoli ed esagoni sono gli unici poligoni regolari che possono tassellare, il che significa che si incastrano su una superficie piana senza lasciare spazi vuoti. Mentre i quadrati risolvono il problema dello spazio, un quadrato richiede un perimetro più lungo di un esagono per racchiudere la stessa quantità di area, rendendolo meno efficiente in termini di cera.
Il Perfetto Equilibrio dell'Esagono
L'esagono è la scelta superiore perché sia tassella perfettamente sia ha il perimetro più corto di qualsiasi forma che possa farlo. Questo principio è così fondamentale che è stato dimostrato matematicamente nella "Congettura del Nido d'Ape" nel 1999. È il compromesso ideale, fornendo il massimo stoccaggio con il minimo costo di materiale.
Comprendere i Compromessi e le Sfumature
Mentre ammiriamo la geometria perfetta del favo, il processo è meno legato al fatto che le api siano architetti esperti e più al fatto che sfruttano la fisica.
Non È Geometria Consapevole
Le api non misurano consapevolmente gli angoli. Questa struttura esagonale è una proprietà emergente guidata dall'istinto e dalle forze fisiche. Le api costruiscono celle approssimativamente circolari vicine tra loro.
Il Potere del Calore e della Pressione
Il calore generato dai corpi delle api ammorbidisce la cera. La tensione superficiale e la pressione delle celle circostanti poi tirano le strutture circolari nella forma più stabile ed energeticamente compatta possibile—una perfetta griglia di esagoni.
Un Incredibile Rapporto Resistenza-Peso
La struttura finale è una testimonianza di design efficiente. Gli angoli di 120 gradi in cui si incontrano le pareti delle celle sono ideali per distribuire lo stress in modo uniforme. Questo permette a un favo che pesa solo 100 grammi di sostenere fino a 4 chilogrammi di peso, un notevole risultato di ingegneria naturale.
Come Applicare Questo al Tuo Progetto
I principi alla base del design del favo non sono limitati alle api. Offrono potenti lezioni per l'ingegneria, il design e la logistica.
- Se il tuo obiettivo principale è l'efficienza dei materiali: Usa forme con il rapporto perimetro-area più basso che possano tassellare, con l'esagono come scelta ideale.
- Se il tuo obiettivo principale è la resistenza strutturale: Distribuisci i carichi attraverso pareti condivise e angoli geometrici stabili, proprio come fa un favo.
- Se il tuo obiettivo principale è massimizzare la densità: Assicurati che il tuo design utilizzi forme che tassellano, eliminando qualsiasi spazio sprecato tra le unità.
Il favo si erge come una masterclass nell'ottimizzazione, dimostrando come semplici principi fisici possano produrre strutture straordinariamente robuste ed efficienti.
Tabella Riepilogativa:
| Requisito | Perché gli Esagoni Eccellono |
|---|---|
| Massimizzare lo Stoccaggio | Tassella perfettamente, lasciando zero spazio sprecato tra le celle. |
| Minimizzare il Materiale (Cera) | Ha il rapporto perimetro-area più corto di qualsiasi forma tassellante. |
| Garantire l'Integrità Strutturale | Gli angoli di 120 gradi distribuiscono lo stress in modo uniforme per un'incredibile resistenza. |
Ispirato all'efficienza del favo? In HONESTBEE, applichiamo gli stessi principi di ottimizzazione e durata ai nostri prodotti per l'apicoltura. Forniamo ad apiari commerciali e distributori di attrezzature per l'apicoltura gli strumenti robusti e di alta qualità necessari per costruire un'attività forte e produttiva. Discutiamo come le nostre soluzioni focalizzate sul commercio all'ingrosso possono rafforzare la tua attività. Contatta il nostro team oggi per un preventivo!
Prodotti correlati
- Fogli di fondotinta in cera d'api Fondotinta d'alveare per la vendita all'ingrosso
- Fondazione di plastica per api di grado alimentare per telai di api
- Preparazione professionale del telaio: L'incastonatore a filo elettrico HONESTBEE
- Macchina elettrica di fondazione della cera d'api con il vassoio di funzionamento e il rullo di fondazione della cera
- Raschietto professionale per miele in silicone a manico lungo per l'apicoltura
Domande frequenti
- A cosa serve il favo di cera d'api? Una guida per una gestione efficiente dell'alveare
- Cosa succede dopo che il processo di appiattimento e goffratura è completo? Dal Cera Fusa alla Base Solida
- Come si installa il foglio cereo e quali sono le sue caratteristiche? Migliora la salute dell'alveare in modo naturale
- A cosa servono i fogli di cera d'api? Una guida per una gestione efficiente dell'alveare
- Cos'è il "foglio cereo" in apicoltura e perché viene utilizzato? Ottimizza la gestione dell'alveare e la produzione di miele
